Reinhart-Rogoff vs. New Zealand: Final Round?

New Zealand’s rugby players celebrate with the traditional Haka after winning the rugby gold medal. (AFP)

After having posted several times on the Reinhart-Rogoff 2010 (RR, NBER and AER versions) vs. Herndon-Ash-Pollin 2013 (HAP) controversy (posts 1, 2, 3, 4), in particular with respect to the prominent role that New Zealand 1946-1951 played in their results, I want to come back (hopefully) one final time to wrap up the outstanding issues. I have benefited from extensive email correspondence with several people much more knowledgeable about New Zealand’s economic history and its statistical representation than I was when I got involved in this question, in particular Jean-Bernard Chatelain (Université Paris I), Jeff Cope (Statistics NZ), Brian Easton (economist and statistician, NZ), Viv Hall (Victoria University of Wellington), John McDermott (Reserve Bank of NZ), Keith Rankin (economist and economic historian, NZ),  Mark Sadowski (University of Delaware), and Bart van Ark (Executive Vice President & Chief Economist, The Conference Board).

I come to praise Reinhart-Rogoff (RR), not to bury them.

This backhand compliment out of the way, let me start by actually praising them.

1.      RR must be thanked for compiling vast databases on financial crises, debt and economic growth. By compiling such comprehensive, worldwide data over such a long period, RR have convincing demonstrated that the present ‘Great Recession’ is not a black swan event at all. And that possibly we can learn something from previous events of a similar character (although, as we shall see, we have to be extremely cautious about how we go about this).

2.      Using these databases they have formulated important conjectures that have, for better or worse, played a major role in the political discussion.  In particular,

a.      They have conjectured that recovery from major financial or banking crises is significantly slower than recovery from ‘normal’ recessions;

b.      They have argued that high levels of public debt are very inimical to economic growth, and, either as an artefact or a deliberate intention of their studies, the 90% public debt/GDP ratio is some sort of threshold or cliff after which things deteriorate very rapidly. (RR have in fact played a peculiar double game on this issue, sometimes emphasizing the 90% threshold, at other times saying there is nothing “magical” about it. See for instance their 2010 FT , 2011 Bloomberg and 2013 New York Times articles and 2011 Congressional testimony.)

Now that I have actually praised them, I’ll cut to the quick to some critical issues that I think everyone can now agree on, but will not dwell on any further here:

1.      Regardless of the methodology or data used, there is a rather weak inverse correlation between growth rates and public debt ratios (it’s actually much stronger at very low debt ratios – under 30% -- than at very high ones, and nothing is said about the direction of causality);

2.      There is absolutely no evidence for a debt cliff or threshold at 90% or any other value (a point I made in my post on dragons, and is summarized here in econometric detail).

3.      Despite this inverse correlation, there is still remarkably high dispersion in the data, so that countries have existed e.g. with debt ratios of 150% and +6% growth, and 180% and -5% growth.

Now to New Zealand

The public debt/nominal GDP ratio

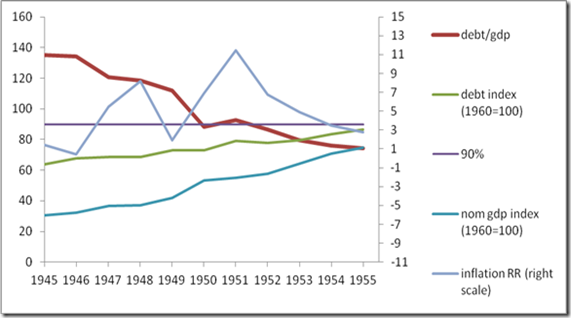
One can rightly ask why such a small and peripheral country should play such a disproportionate role in a study on debt and growth in the entire Western world in the post-war period. In the interwar period this is perhaps more obvious, since NZ attained a total public debt ratio of all of 249% in 1933. But for the RR 2010 paper we are only concerned with the period 1946-2009, when NZ only had a debt ratio over 90% for a few years immediately after the war. These were 1946-49 and 1951, see Figure 1 (1950, when the ratio dips to 88%, is a case I will come back to). While seven countries experienced debt ratios over 90% in RR’s database, of varying length (up to 19 years for the UK and Greece), NZ is catapulted into prominence because of several peculiar aspects of RR’s methodology. First, they only use the 1951 observation and leave out 1946-9 (as they later explained, the debt ratios for these years were not yet available, although it should have been clear that they were over 90%). Second, RR take each country’s growth experience in a debt category as a single observation by averaging over all that country’s years, instead of retaining each country-year as an individual observation. Thus NZ counts as 1/7^th of the high-debt observations, as much as the UK and Greece, even though it only has one year in the category. Finally, the growth rate of real GDP for the one year they do use, 1951, based on the Maddison 2010 database, is exceptionally low (minus 7.6%). Given that the other NZ years of high debt had some very high growth rates, these factors in concert severely depress the mean and (somewhat  less) the median of the sample growth rates for debt ratios over 90%. Simply inputting the other four NZ high-debt years and weighting all country-year observations equally, as HAP show, boosts the mean growth rate of high-debt countries by over 2%.

 

Figure 1 New Zealand public debt dynamics 1945-1955. Indices are for nominal values of debt and GDP. Computed from RR’s original spreadsheets from HAP/UMass website. 90% is RR’s dividing line for high debt ratios. Inflation rate in per cent, right scale. Notice the jig the debt ratio makes around 90% in 1950-51 during wool boom take-off.

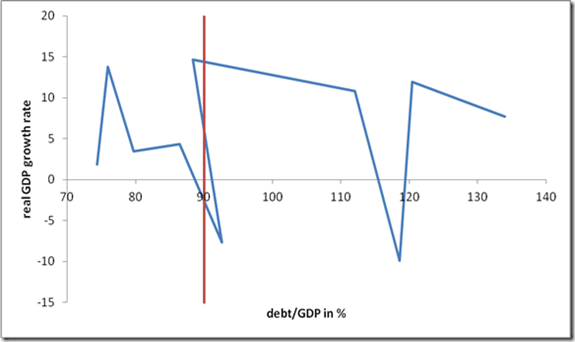
Figure 2 Debt ratio vs. real GDP growth rate (based on Maddison 2010 data as employed by RR 2010) for NZ 1946-1955. The 90% line self-selects high growth in 1950 into the lower debt category but returns the low growth rate of 1951 into the high debt category, although the absolute debt level was unchanged.

There is one more curious artefact of RR’s treatment of the NZ 1946-51 data that needs to be addressed that as far as I know has not been mentioned by HAP or anyone else. The year 1950 falls out of the 90+ debt category only to return to it in 1951, not because the debt had been reduced in absolute level (it was exactly unchanged! – see Figure 1) but rather because of the high growth rate in that year. Remember that RR are correlating debt ratios, i.e., nominal debt/nominal GDP, with real GDP growth rates, and this ratio will fall if either debt falls or nominal GDP rises. In the period 1946-51 NZ is by chance rapidly reaching the critical bin boundary of 90%, so that the growth rate becomes a self-selecting trigger determining if NZ is counted in the 90+ category or the more benign 60-90% one. High growth in 1950 shoves it to the left, low growth in 1951 shoves it back to the right, even though the debt level is unchanged, so we now have causality running clearly from growth to the debt ratio in such a way that a year with high growth does not get counted as high debt, but the following year with low growth does. This is a very funny and certainly unintentional artefact of the RR methodology of imposing a rigid bin boundary at 90% and correlating two variables that both depend (inversely) on GDP, as well as the adventitious fact that NZ just happens to be at the 90% value in this period. Near the bin boundaries RR’s methodology automatically sorts the data into high debt/low growth and lower debt/high growth subcategories if the absolute debt level is constant.  If we restore 1950 to the high-debt sample (the ratio dips briefly to just below 88%), the average growth rate for years in which NZ has a debt ratio above “90%” rises from -7.64% (just the year 1951, as in RR 2010) to 2.57% (1946-49+1951, as in HAP) to 4.59% (all six years 1946-1951). Thus if we really want to weight the NZ data from this period as strongly as RR’s methodology compels, we can make an even stronger case for high mean growth rates in the 90+ category than even HAP were prepared to make. Including 1950 in the sample boosts NZ mean growth by another 2.02% and boosts the result for the entire country sample (using RR’s original country weighting method) by another 2.02%/7=0.29%.

Thus exactly at the bin boundaries the much-discussed issue of the direction of causality—from debt ratio to growth or vice versa—can become highly amplified in RR’s counting procedure, as the NZ jig at 1950 illustrates. It remains to examine to what extend this might also apply to other countries and years.

Wool boom and industrial unrest

Before examining the data issues, let us begin with the undisputed facts about this period in NZ economic history. First, the economy took off at the end of the 1940s, and particularly with the outbreak of the Korean War in June 1950, because of the wool boom (Figure 3). Economists call this a terms-of-trade shock, when the price of a major export commodity suddenly rises, generating windfall profits and desperate attempts to increase production (to the extent that children would apparently be sent out to gather wool caught on the barbed wire fences). As a pastoral product, however, wool supply is highly inelastic in the short run, so nominal and real income effects can diverge, resulting in inflation.

Figure 3 This Gordon Minhinnick cartoon, published in The New Zealand Herald in November 1950, alludes to the wool boom that resulted from the Korean War. The man with the glasses is then NZ PM Sid Holland, followed by NZ average citizen. (Source: Te Ara/Encyclopedia of New Zealand).

According to the Te Ara/Encyclopedia of New Zealand,

… the Korean War had an enormous economic impact on New Zealand. It precipitated a boom in wool prices that led to a stupendous influx of money into the country, leaving farmers more prosperous but unsettling the rest of society as inflation affected the cost of living. When an industrial dispute on the waterfront threatened this bonanza in 1951, the government declared a state of emergency and used the armed services to load cargo.

Wool prices tripled in 1950 in response to American stockpiling (see Figure 4), but a price ceiling imposed by US authorities early in 1951 caused prices to fall back again by 50%. At the same time, partly as a result of the inflationary situation induced by the wool boom, the waterfront workers were locked out by the government (they had been offered only a 9% wage increase while other unions had agreed to 15%). Sympathy strikes spread to coal mining, meat freezing, railroads and hydroelectric industries (see my post “One strike and you’re out”, which sparked my interest in this subject).

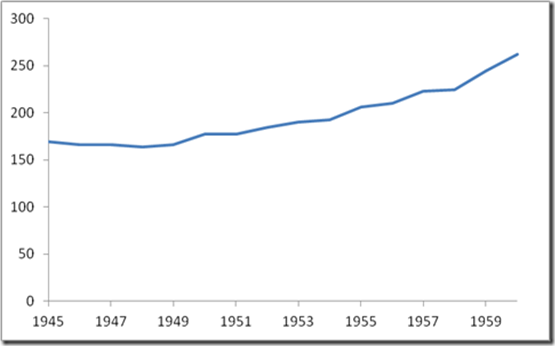
Figure 4 NZ wool price index. The wool boom already starts at the end of the 1940s and peaks briefly in 1951. (Source: SNZ)

Figure 5 NZ wool production, 1000 tonnes. (Source: SNZ)

However, the volume data in Figure 5 indicate that the wool boom was more a price than a quantity phenomenon. The rise is very gradual, and there is no volume decline after the price peaks in 1951. So at least for this important component of exports, real output shows no volatility at all. The volatility is entirely in the price. What we cannot exclude, however, is that the income effects induced by the price volatility had no real repercussions on production in other sectors (as well as on imports).

Real GDP chronologies

Now, for the purposes of RR’s study of debt and growth, we need time series for nominal GDP (to compute the debt/GDP ratio) and real GDP (to measure performance). The difference between the two growth rates will be the inflation rate. RR obtain their real GDP data for NZ from the well-known Maddison 2010 database, but turn to other sources for their RRR 2012 paper. A second series is available from Statistics New Zealand in their Long Term Data Series (LTDS) (note that SNZ did not begin compiling official time series according to the UN’s System of National Accounts until 1955). And recently a quarterly series has become available from Hall and McDermott 2011 (HM).

In previous posts I talked about a “post modern nightmare” of data incompatibilities and inconsistencies. It gets worse, but it also gets better. I’ll list some items of confusion and how they can be resolved.

1.      Both the Maddison (after 1939, see his Monitoring the World Economy, OECD, 1995, p. 134) and the SNZ real GDP series are for NZ fiscal years, not calendar years.  A NZ fiscal year in the relevant period is April 1- March 31.

2.      However, Maddison dates his year from the starting day, and SNZ from the ending day of the fiscal year. This explains why these data series are shifted by one year. Thus for Maddison, fiscal year April 1, 1951 to March 31, 1952 counts as 1951, while for SNZ it is 1952. Hence any methodology that critically depends on annual chronology can easily become misspecified by not recognizing that these are fiscal years, 9 months of which fall into the first calendar year, and 3 months of which fall into the next one, and different statisticians can choose which calendar year they assign them to. This explains why 1951 is a recession year for Maddison but only 1952 is for SNZ, even though they are talking about the same fiscal year and same recession. In terms of synchronicity with the calendar, Maddison is still the preferred series, and the SNZ series should be moved up one year when it is a question of high-frequency timing. Since RR are correlating contemporaneous annual debt ratios and growth rates, this is not unimportant in getting things right.

3.      The SNZ “Maddison Index” of real GDP on its LTDS has a typo error for 1946 (they give 219.9 instead of the original value of 217.9 from Maddison’s Monitoring the World Economy, OECD, 1995, and carried over into the online 2010 database). Since I was using the SNZ LTDS-Maddison Index instead of going back to the Maddison source, this led me to suggest that RR had also made a transcription error resulting in slight discrepancies (+-1%) in the NZ growth rates for 1946 and 1947. I apologize for this aspersion to RR’s already much maligned integrity – the error was SNZ’s, and they have already corrected it in the LTDS table (personal communication Jeff Cope).

So what do the GDP time series show about NZ in the early post-war period? Figure 6 graphs the growth rates in real GDP from the different sources.

Figure 6 NZ real GDP growth rates: quarterly data from Hall & McDermott (2011), annual data from Maddison (2010) and SNZ $90 constant price series shifted forward one year.

Growth rates are computed from the quarterly HM data in three ways. First, I compute the annual growth rate from a quarter and the previous year’s same quarter. Second, I compute the growth rate from one quarter to the next one, annualized. Finally, I take a running sum of four quarters and compute the growth rate to that sum one year previous. The Maddison annual growth rates are applied to the four quarters in that fiscal year (thus Maddison 1950 applies to 1950q2-1951q1), and are compared to SNZ $90 year 1951 (encompassing the same four quarters 1950q2-1951q1).

If we take the HM growth rates as both the highest frequency and most chronologically exact representations, then we see that the three sources are fairly consistent internally and make sense in terms of what we know about NZ economic history. The wool boom, perhaps somewhat surprisingly, already takes off in the second half of 1949, even before the outbreak of the Korean War, and peaks in early 1950. The economy then goes into recession in the first quarter of 1951, when we know that both the waterfront lockout/strike and the wool price ceiling occur.

Thus, to the extent that RR’s study requires a precise annual correspondence between debt ratios and real growth rates, the Maddison data as is or the SNZ $90 shifted forward one year are perfectly acceptable, though Maddison shows higher peaks in 1946 and 1947 and a lower trough in 1948. The 1951 recession is reconcilable between them once the respective datings of the fiscal year are understood, and they synchronize well with the three ways of extracting growth rates from the HM quarterly data. The conclusion stands in contrast with the approach RR take in RRR 2012 (Journal of Economic Perspectives), their May 5, 2013 data errata, and in their response to critics, “A Note on Data for New Zealand” April 27, 2013 post:

Poring over the time series we used in late 2009 for RR (2010) "Growth in A Time of Debt", it became apparent that the New Zealand GDP data used has an error. It is off by a year. The source of the problem on New Zealand is the original Maddison data. This has propagated over time.

The Total Economy Database at the Conference Board now updates the Maddison data and still has the error, at least as late as April 27, 2013. I have notified the Conference Board of the error.

Note that this does not affect the Journal of Economics Perspectives paper on "Debt Overhangs", where the data for the 1861-1979 comes from the New Zealand Statistics Office…

RR seem to have fallen victim to a misreading of how Maddison and SNZ date their annual series, and that they both refer to fiscal years April 1 – March 31 but with different years attached to them, which explains the one year shift. And from our comparison with the quarterly HM data it is clear that the Maddison data they used in their 2010 paper are closer to chronological time, and it is in fact the SNZ data that needs to be shifted up one year. Thus it appears that the RRR JEP paper needs to be revised and not the Conference Board’s administration of the Maddison database. Bart van Ark will be publishing a note on these questions in the near future on the Maddison project website.

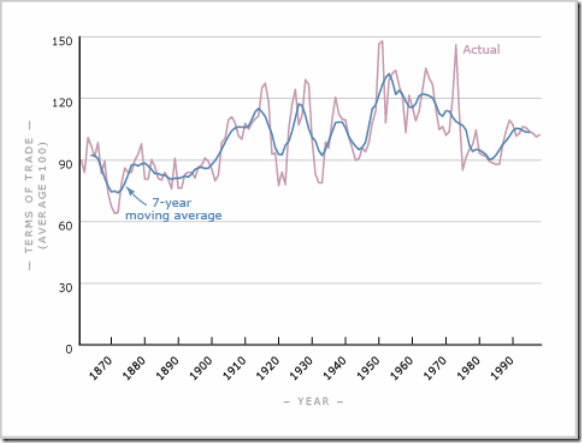
But can the extreme volatility of any of the real GDP growth rates for this period be believed? As we saw in Figure 4, the fluctuations in wool export prices, NZ’s primary export commodity, seem to be driving the economy in what is well known to economists as a terms-of-trade windfall (and subsequent crash). Looking at NZ’s overall terms of trade, we see the same pattern:

Figure 7 New Zealand’s overall terms of trade, annual data and 7-year moving average. (Source: SNZ and Encyclopedia of New Zealand)

The largest peak and crash occur in 1950/51, as we expect. To what extent are these extreme fluctuations merely driving nominal quantities as opposed to real output, and thus manifesting themselves primarily in inflation? A high proportion strikes me as extremely likely, especially in view of the few direct observations of volume indices such as wool production (Figure 5), or tallies of export tonnage (the NZ 1954 statistical yearbook records only a small decline of about 3% for 1951). This is a well-known problem in national accounts: when relative prices fluctuate significantly in a short time interval, it is difficult if not impossible to extract sensible changes in real quantities just using price deflators. (This also played a role during the energy crisis in the 1970s, where the apparent decline in productivity growth may partly be an artefact of such statistical anomalies.) Since we know that inflation took off in NZ in this period and contributed to the industrial unrest, I think it reasonable to assume that the fluctuations in real GDP growth were much more modest or even nonexistent than any of the available time series suggest. While a good case can be made that a contraction did take place in 1951, it seems unlikely that it was as large as -7.6% in real terms (nor that the preceding boom was +14%). And experts on NZ history still seem at a loss to decide how to apportion any real decline in 1951 between the disruptions due to the waterfront lockout/strike and the decline in the wool price and its knock-on effects.

In the end it is subtle shortcomings of RR’s methodology that thrusts the NZ experience accidentally to such a prominent position. These shortcomings are

1.      Using just four bins for debt ratios instead of a much finer resolution, or disposing of binning entirely in favor of a fully formulated econometric specification or (semi)parametric estimator;

2.      Correlating contemporaneous annual observations of debt ratios and growth rates instead of using moving averages of the time series. As we have seen, the bin boundary dynamics plays subtle tricks when a country’s debt ratio nears the boundary, self-selecting high-debt ratio/low growth pairs. NZ just happened to fulfil this criterion around 1950. And these historical time series (whether Maddison’s or any other source) are simply not accurate enough on an annual basis nor were they ever intended to support such fine tuning.

3.      Not explicitly investigating causality by investigating a lag structure running one way or the other (although RR 2010 claim that lags had no effect on their original result without discussing the evidence).

4.      While one can make legitimate arguments in favor of using average country growth rates in each debt ratio category instead of exploiting all country-years, for the dataset RR 2010 employ, this leads to the obvious deficiency that the small number of high-debt ratio observations for NZ (one, five, or six, as you choose) propel NZ into too crucial a role in determining the aggregate outcome. And NZ is obviously too small and peripheral a country to carry the burden of such a wide-ranging conclusion about the role of debt in long-term economic growth. Moreover, as we have seen, NZ’s growth experience 1946-51 is completely idiosyncratic and has nothing whatsoever to do with its debt ratio (which did not seem to be of any great concern to anyone at that time, and had been more than twice as high just 15 years earlier). Rather, it was driven by the vicissitudes of post-war demobilization, the wool boom/Korean War/terms-of-trade volatility and their resulting inflation, and a massive instance of labor unrest which came out of them. Abstracting from these historical vicissitudes in such a crude statistical study will always be inherently risky, even if no blatant data errors had been committed.

In one sense one could say that NZ’s role in this affair was fortunate, for it led to the exposure of a problem of greater significance in all quantitative science: how to guarantee the transparency and integrity of scientific research. Only the failure of many economists to reproduce RR’s original results eventually led to the necessary access to and scrutiny of RR’s data and methods. HAP have to be thanked for taking this thankless task onto themselves, but the chasm of quantitative abjectness this revealed (whether it affected the results significantly or not is entirely irrelevant) was simply breathtaking.

As someone who does economic modelling myself and has even dabbled in econometrics occasionally, I am all too familiar with the scope for making simple but discrediting errors, and thus have some sympathy with RR’s plight. However, that this paper could be so prominently published without peer review and making the data and spreadsheets available on the web (or at a minimum on request from other researchers) for three years, is really disturbing. It threatens to discredit all serious analytical thought in the popular mind, and not unjustifiably. The economics profession will have to devote more thought and rather quickly to devising reliable institutional procedures for guaranteeing transparency and integrity (see also Barry Eichengreen’s recent article on this issue, which perhaps downplays the question of intention, as I point out in my comment).

On the other hand, were it not for the incentives RR gave the profession to scrutinize the trials and tribulations of New Zealand during the immediate post-war period, we might still be the victims of oversimplistic and ahistorical threshold and causality delusions regarding the public debt-growth nexus (for the latest on that debate, see RR’s May 25 letter to Paul Krugman and the latter’s May 26 blog back).

USA vs. Eurozone: How Many Differences Can You Spot Between These Two Pictures?

How many differences can you spot between these two pictures?

George Soros and Hans-Werner Sinn have been at each other again at Project Syndicate (see my previous two posts on this debate).

While Soros pleads for debt mutualization in the form of Eurobonds as a necessary (but possibly insufficient) condition for Eurozone stability, Sinn reiterates that this is not legally possible under German law nor corresponds with Germany's original intentions in agreeing to the Maastricht Treaty.

I just want to briefly mention a different point Sinn brings up in which he betrays a serious gap in his knowledge of American history and that country's experience with its currency union (otherwise known as the US Dollar, the longest running successful currency zone in history). The first US Treasury Secretary, Alexander Hamilton, mutualized the 13 state debts left over from the Revolutionary War and established the US National Debt based on centrally levied tariffs and a whiskey tax. Many observers have argued that the Eurozone must also go through its "Hamilton moment" before it can graduate to a fully functioning currency zone.

Sinn claims, in contrast, that

George Soros underestimates the risks that debt mutualisation would pose for the future of the eurozone. When Alexander Hamilton, the first US finance minister, mutualised state debts in 1791, he thought this would cement the new American nation. But the mutualisation of debt gave rise to huge moral hazard effects, inducing the states to borrow excessively. A credit bubble emerged that burst in 1838 and drove most of the US states into bankruptcy. Nothing but animosity and strife resulted.

This is a very curious statement, since the US currency zone, when I last looked (and the Republicans hadn't played chicken again with the debt ceiling, their symbolic legislative blackmail weapon), was still going strong after over two hundred years, its creditworthiness still intact, and no Federal state now has a debt burden over 19% of its GDP. 75% of US public debt is Federal, not state, supported by a 19% central government revenue rate on GDP. In the Eurozone, less than 1% of GDP is collected by Brussels as taxes, and there is no central sovereign debt (except for a minor amount issued by the European Investment Bank) but 17 national sovereign debts (not counting the EU countries not using the Euro). In other word, the US is a model of a functioning currency union, while the EU is still stuck in a time warp around 1791. Have "most US states" ever been driven into bankruptcy, and has this been a source of "nothing but animosity and strife"?

A good source of data on US state defaults is at LearnBonds. The first state defaults were in 1841 (9 in all, not "most states", and not 1838), 50 years after Hamilton created the National Debt (the Euro should live so long!), the last in 1933. There was also a wave of six defaults of defeated Southern states after the Civil War in 1870. That's it. Nothing like Sinn's "animosity and strife" (the Civil War was not fought about the 1841 default wave, by which time the problems had already long been repaired). So we are really only talking about the default wave of 1841.

A good paper on this episode is "Debt, Default, and Revenue Structure: The American State Debt Crisis in the Early 1840s". The authors conclude that

1. very few of these states fully defaulted on their debts with actual losses for creditors;
2. these nine states returned successfully to bond markets within a few years;
3. the cause of the default wave was not any moral hazard created by Alexander Hamilton 50 years earlier but the laissez-faire economic policies of the Jackson era. The debts had been raised to finance highly sensible infrastructure projects, but the tax systems of the Western states were not sufficiently developed at that time to support the debt burden. None of these states were bailed out by the Federal government, nor had any of them taken on the debt in the expectation that they would be.

It has become increasingly clear that a currency zone can only function with mutualized sovereign debt supported by a central fiscal and tax structure, and a banking union (the latter something the US only really introduced in 1933 with Federal deposit insurance - before that the US was subject to recurring massive bank runs). Paul de Grauwe, Europe's foremost expert on currency zones, has just restated the case for a European Hamilton Moment at Project Syndicate.

Sinn is within his rights to reject this solution, but then Soros has a point that Germany should be consequential and leave the Eurozone if it can offer no better constructive solution. But Sinn should not invoke a caricature of American history to repeat ad nauseam the strained shibboleth of moral hazard (an important issue) to justify his solution: 20-30% debt-deflation in the EZ periphery, or, as we Americans remember from the Vietnam war, "we had to destroy them to save them."

Quote of the Day: Austerity and Public Health

What we have found is that austerity — severe, immediate, indiscriminate cuts to social and health spending — is not only self-defeating, but fatal.

DAVID STUCKLER and SANJAY BASU, "How Austerity Kills", op-ed in today's New York Times

Brüning and Mellon Memorial Prizes Awarded in Vienna, May 11, 2013 (special photo report)

Vienna city hall (left) and Creditanstalt (above), venues for the prize ceremonies.

[from our Krämerzeitung Special Society Correspondent, Vienna, May 12]

The prestigious Heinrich Brüning and Andrew Mellon Memorial Prizes, created by the 'Creditanstalt', were awarded last night in a gala event attended by many notable celebrities. The date commemorates the historic May 11, 1931 resolution of the Creditanstalt Bank, which set off the worldwide chain of bank failures and currency runs that really made the Great Depression the profound event we cherish today.

The Prizes were awarded by Lithuania's President Dalia Grybauskaitė in the name of all European creditor states and their banks (shown here receiving the Charlemagne Prize last week in Aachen). 

President Grybauskaitė praised the recipients for their tireless efforts to impose debt-deflation on deserving economies, and said the sacrifices would be amply rewarded in the long run when we are all dead. (Gadfly socialite historian Niall Ferguson was overheard remarking that this was easy for her to say, Madame President being childless and unmarried. Since his recent experience of eating crow, however, he wisely refrained from speculating about her sexual orientation. He could not restrain himself from remarking, though, that if only more British tourists had bought Hitler's artistic postcards while he was peddling them on these very Viennese streets, the 20th century would have turned out quite differently, so the British have only themselves to blame for WWII.)

Historian-about-town Niall Ferguson was decked out for the occasion but exercised remarkable restraint in speculating about  participants' sexual orientations.

European Commission Vice-President Olli Rehn was then awarded the Heinrich Brüning Memorial Prize for Self-Defeating Macroeconomic Stabilization Policy (aka Austerity). In accepting the award, VP Rehn stated that he could now see "light at the end of the debt-deflation tunnel" once essential "structural reforms" were finally implemented by the ailing countries.

Olli Rehn seeing "light at the end of the debt-deflation tunnel" once France liberalizes advertising for veterinarians and Italy extends shop opening hours (Der Spiegel 20/2013).

The joint award of the Andrew Mellon “Liquidate labor, liquidate stocks, liquidate farmers, liquidate real estate” Memorial Prize for the Expeditious Resolution of Banks (aka Bank Runs) to Finance Ministers Wolfgang Schäuble and Jeroen Dijsselbloem was a source of considerable merriment. IMF Director Christine Lagarde had to engage in all-night, one-on-one negotiations with the two recipients (reportedly including games of hopscotch and pick-up-sticks) to strong-arm them into reaching a sharing agreement that was a precondition for the award. The troika announced that Schäuble would receive 10.9%, Dijsselbloem 6.9% of anything left of the One Million 'Cypriot Euro' prize money after the Central Bank of Cyprus and the ECB take their cut for 'widows and orphans.'

Madame Lagarde in tense one-on-one, all-night negotiations with Jeroen Dijsselbloem (left) and Wolfgang Schäuble (right). Madame Lagarde's press secretary hastened to add that the IMF Director had neither smacked Dijsselbloem in the eye nor kowtowed to Schäuble to reach the agreement.

Dijsselbloem and Schäuble later showed themselves to be "a heart and a soul."

The closing ceremony of the 'Creditanstalt' Memorial Prize Awards received an enthusiastic standing ovation from the international states-persons in the audience.

Runner-up candidates put on a brave face to hide their disappointment.

After the formalities were over the distinguished audience eagerly disappeared into the famed Vienna nightlife.

Lithuania's President Dalia Grybauskaitė Will Present Brüning and Mellon Prizes in Vienna on Saturday

Breaking News!

Lithuania's President Dalia Grybauskaitė receiving the Charlemagne Prize in Aachen today

Lithuania's President Dalia Grybauskaitė, who has just received the Charlemagne Prize of Aachen for her successful austerity policies in her country, has agreed to present the Heinrich Brüning and Andrew Mellon Prizes in Vienna on May 11. The 'Creditanstalt' Award Committee was able to induce her to extend her stay in Central Europe to serve in this important capacity. 

The Award Committee is convinced that no one is better fitted to present these prizes than the Lithuanian President, who in her acceptance speech stated that

Today Germany plays the leading role in ensuring European stability and does not allow us to wander from the path of trust in Europe. That is why it is Germany which gets the strongest criticism – and also our deepest respect. [reported by 15min.lt]

European Parliament President Martin Schulz, in his congratulations, praised the Lithuanian president, saying that she says what she means, is not afraid to speak her mind, calls a spade a spade, has low tolerance for bureaucracy, is a tough negotiator and knows how to kowtow appropriately to Germany. [15min.lt] These qualities undoubtedly played some role in selecting her for the Charlemagne Prize.

President Dalia Grybauskaitė is thoroughly familiar with this year's prize recipients, Olli Rehn for the Brüning Prize, and Wolfgang Schäuble and Jeroen Dijsselbloem for the Mellon Prize, from her term as a European commissioner.

In presenting the two 'Creditanstalt' Prizes, she is expected to highlight her economic success in Lithuania as a model for other crisis countries, where real GDP, after first declining by 15% in 2009, has now recovered to just 5% below its 2008 value, while the population, by exporting small children as biofuel to Germany, could be reduced by all of 10% (the latter measure being inspired by Ireland's great success with Swift's A Modest Proposal).

The 'Creditanstalt' will be most happy to welcome President Dalia Grybauskaitė to its historical quarters on Saturday for the award ceremony.

Imperial Ingratitude: No Homosexuality Please, We're British

A trinity of British homophobia victims: mathematician Alan Turing (upper left), economist John Maynard Keynes (right), poet and playwright Oscar Wilde (lower center)

Niall Ferguson's recent smear of J.M. Keynes, which, particularly in the context of his previous writings, represents Keynes as an effete homosexual whose childlessness was behind his economic doctrine's supposed inflationary bias and disregard for the long run and whose fantasized infatuation with a Jewish German banker led him to an almost treasonous sympathy (in Ferguson's creative reconstruction) for the plight of post WWI Germany, is unfortunately only a revival of a very sorry British tradition. (While Ferguson has since apologized for the "stupidity and insensitivity" of his remarks, he still insists on seeing Keynes' thought through a sexual lens.)

I'll call this tradition Imperial Ingratitude. While Keynes himself did not seem to suffer from any homophobic discrimination during his lifetime, the same cannot be said of his compatriots Alan Turing and Oscar Wilde, the latter providing the original template for British homosexual persecution and public disgust.

Why ingratitude? Alan Turing and John Maynard Keynes are undoubtedly the two British intellectuals who most contributed as individuals to saving Western Civilization from itself in the 20th century. (And of course Oscar Wilde was one of the English language's outstanding writers.) Yet Turing was arrested and convicted of homosexuality (still a crime in 1952 Britain) and sentenced to female hormone treatments as a then pseudo-scientific cure for the 'ailment.' He died of cyanide poisoning in 1954, whether by accident or suicide is still being debated.

Turing was central to the British cryptanalysis efforts at Bletchley Park during World War II that played a crucial role in defeating the German military, particularly during the Battle of the Atlantic (the breaking of the German Enigma and Geheimschreiber cipher machines was only revealed in the 1970s). Churchill's "Never in the field of human conflict was so much owed by so many to so few" applies as much or more so to Turing and his fellow mathematicians (and chess players, linguists, and crossword puzzle addicts) as to the RAF pilots it was originally intended for.

And the same is true of Keynes. Not only did Keynes develop the first intellectually respectable theory of why a modern economy could fall into the trap of persistent unemployment such as the capitalist world of the 1930s experienced, he outlined the policy prescriptions of demand management, so at odds with previous received doctrine, that guided the revival from the depths of the depression, the management of war finance, and 'the golden twenty years of capitalism' until the turmoil of the 1970s. And his was not only a theoretical contribution, as he was instrumental in negotiating the postwar system of international economic cooperation - the Bretton Woods Agreement - that attempted to avoid the disastrous disarray of the interwar years (undoubtedly under the influence of his German banker infatuation). And for all this he deserves to be smeared as an effete childless homosexual by the likes of Niall Ferguson (the fact that he died of a heart attack soon after returning from strenuous negotiations in 1946 is no doubt just further proof of how little he cared about future generations)?

In the end, what were the crimes of Turing and Keynes? Picking up working class men seems to be the most diabolical, in the eyes of both the 1952 Manchester court that convicted Turing and Niall Ferguson ("this is a time in Keynes's life of considerable homosexual activity: a bizarrely meticulous list of sexual encounters from 1915 suggests that he had at least eight male partners in 1911 (including 'liftboy of Vauxhall') ..."). Exactly the crimes of Oscar Wilde that led to his conviction for 'gross indecency' and two years of hard labor in 1895.

Liberal industrial capitalism and a multilateral trading regime ('globalization') such as the world has known up to World War I and after World War II have been unprecedented machines for lifting mankind out of poverty and ignorance. But they have not been without their pitfalls. The concentration of wealth among the few, the burdens of the business cycle borne by the many, financial meltdowns, collapses of international trade, mass unemployment, and conflagrations between rivalrous imperialist powers have been some of their more unfortunate side effects.

By chance history chose two flagrant British homosexuals with exceptional intellectual gifts and penchants for picking up working-class men to save Western Civilization from itself. I think a little respect from posterity is not too much to ask.